1. Wat is cryptografie
Als twee personen geheime informatie geheime willen uitwisselen dan zou je je dat zo kunnen voorstellen. Alice verstuurt haar informatie in een afgesloten box wat ze met haar sleutel op slot draait. Bob heeft ook zo'n sleutel en kan de box weer openen. We noemen dit proces encryptie. Onderweg kan niemand bij de informatie (is dat zo?).
Bij encryptie draait het om de sleutel. Hoe krijg je de sleutel veilig bij Bob? In deze cursus zullen hiervoor verschillende technieken worden besproken.
Bekijk het volgende inleidende filmpje.
2. Het Ceasar cijfer
Julius Caesar was een dictator die versleuteling gebruikte om met zijn veldheren in het geheim te kunnen communiceren. We noemen dat subsitutie maar het wordt ook wel het Ceasarcijfer genoemd. De verleuteling vindt plaats door iedere letter van de tekst te vervangen door een vervangende letter in een vaste volgorde.

In het bovengenoemde plaatje wordt een rotatie van 3 gebruikt. Iedere letter schuift 3 plaatsen op.
Hieronder zie je een voorbeeld van een verschuiving van 23 plaatsen.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Bij zo'n verschuiving zijn er 25 mogelijkheden om de juiste verschuiving te vinden. Door deze mogelijkheden uit te proberen kom je vanzelf een keer op de goede versleutelde tekst. Er is echter ook een betere manier. We noemen dit frequentie-analyse. Dit is gebaseerd op het feit dat bepaalde letters in teksten vaker voorkomen dan andere letters.
Neem bijvoorbeeld de volgende tekst:
AWESFV VAW YWYWNWFK GFVWJKUZWHL GX GH BW UGEHMLWJKQKLWWE TAFFWFVJAFYL, EGWL VAW YWYWNWFK FAWL CMFFWF TWYJABHWF.
We weten dat de E het vaakst voorkomt in het Nederlands. We zouden dus kunnen gaan zoeken naar welke letter in bovenstaande tekst het vaakst voorkomt. Als je deze zoekt en deze letter vervolgens terug rekent kun je de tekst snel ontcijferen. IN onderstaand filmpje wordt dit nog eens uitgelegd.
3. Poly alfabetische vercijfering
Beschouw de onderstaande tabel. Deze is bekend geraakt door Blaise de Vigenère en heet daarom de Vigenère tabel.
| |
Vigenère tabel |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| rij |
|
| 0 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 1 |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
| 2 |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
| 3 |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
| 4 |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
| 5 |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
| 6 |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
| 7 |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
| 8 |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
| 9 |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
| 10 |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
| 11 |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
| 12 |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
| 13 |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 14 |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
| 15 |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
| 16 |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
| 17 |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
| 18 |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
| 19 |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
| 20 |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
| 21 |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
| 22 |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
| 23 |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
| 24 |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
| 25 |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
De tabel zijn eigenlijk 25 Ceasarcijfers. In rij 3 is de verschuiving 3 plaatsen. Stel nu dat we de volgende sleutel hebben: LEMON.
En je wilt de volgende zin versleutelen: ONTMOETING IN PARIJS.
De vertaling wordt dan: ZRFABPXUBT TR BOETNE
Dat werkt als volgt:
| |
Vigenère tabel |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| rij |
|
| 0 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 1 |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
| 2 |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
| 3 |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
| 4 |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
| 5 |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
| 6 |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
| 7 |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
| 8 |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
| 9 |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
| 10 |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
| 11 |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
| 12 |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
| 13 |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 14 |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
| 15 |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
| 16 |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
| 17 |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
| 18 |
S |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
| 19 |
T |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
| 20 |
U |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
| 21 |
V |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
| 22 |
W |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
| 23 |
X |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
| 24 |
Y |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
| 25 |
Z |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
De eerste letter is de O. De eerste letter van de key is de L. Vergelijk beide letters met elkaar in de tabel. Dit wordt gedaan in de groene rij (rij 11). In deze groene rij is te zien dat je uitkomt op de Z. De tweede letter wordt de R door de N en de E met elkaar te vergelijken in de blauwe rij. Zo ga je door. b
Wat je hier eigenlijk doet is telkens een andere verschuiving toepassen. Dus bij de L is de verschuiving 11.
Hoe kun je dit nu kraken? In feite is er sprake van meerdere verschuivingen (shifts). Bij de sleutel LEMON gaat het om vijf verschuivingen. Je kunt proberen die verschuiving te vinden omdat deze zich herhaald. Zodra je de verschuiving hebt gevonden, heb je de sleutel en is deze gekraakt.
Dus als volgt:
| origineel |
O |
N |
T |
M |
O |
E |
T |
I |
N |
G |
| versleuteld |
Z |
R |
F |
A |
B |
P |
X |
U |
B |
T |
| verschuiving |
11 |
4 |
12 |
14 |
13 |
11 |
4 |
12 |
14 |
13 |
Je kunt nu zien dat de verschuiving zich herhaald. De key LEMON is nu snel gevonden. Dit is echter achteraf praten want als je alleen het versleutelde woord hebt wordt het lastiger. Met een zin kun je meer letters analyseren en proberen een veelgebruikte letter te vinden. Dat doe je door overeenkomsten te vinden bij de derde letter, bij de vierde letter etc.
Bekijk onderstaande film waarin dit nog eens wordt uitgelegd.
4. Is random random?
We beginnen deze les eerst met een oefening. Ga naar deze link. Ga ervoor zitten, hou je rechterhand bij het numerieke toetsenbord en type met je wijsvinger minstens 500 keer een 0 of een 1. Je zou uit kunnen komen op een volgende uitkomst:
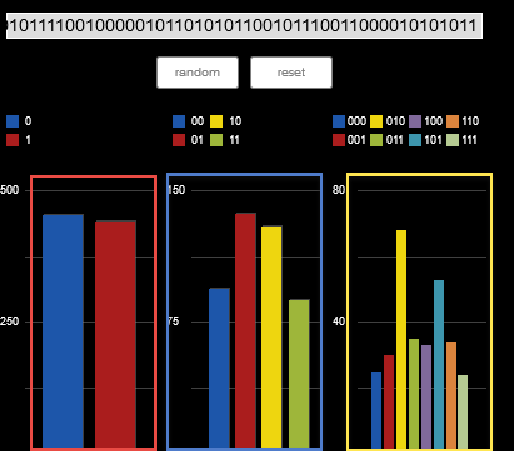
Als we hetzelfde plaatje random maken dan zie je een ander beeld.
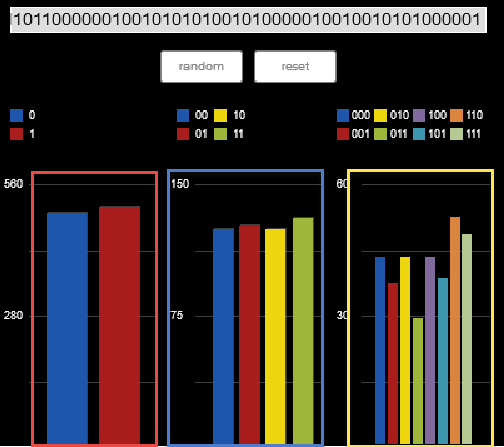
Dit plaatjes zijn als volgt verklaarbaar. Aan de linkerkant (rood omlijnd) zie je het aantal nullen en enen. Dit is in beide plaatjes ongeveer gelijk. Bij de blauw omrande staafdiagrammen zie je het aantal duo's zoals 00, 01 of 10. Je ziet dat bij de menselijke invoer 10 en 01 oververtegenwoordigd zijn. De geel omlijnde staafdiagrammen geven het aantal trio's zoals 001, 101 etc. Bij de menselijke invoer kun je zien dat 010 oververtegenwoordigd is. Dit noemen we een vingerafdruk en we zouden zo'n vingerafdruk kunnen gebruiken om informatie te kraken.
In het navolgende filmpje wordt dit nog eens uitgelegd.
5. De enigma
De Enigma was een machine wat is ontwikkeld om de one-time-pad zoveel mogelijk te benaderen. Om een bericht over te zenden moesten zowel ontvanger als zender dezelfde setting hebben (dezelfde sleutel). 
De enigma wordt ook wel een rotor encryptie machine genoemd. Iedere keer als een letter wordt ingetyped, roteren de letters.
De enigma kon 26 x 26 x 26 verschillende posities produceren. Hiermee kun je 17.576 shifts produceren (ter vergelijking: de poly alfabetische vercijfering uit lesonderdeel 3 heeft er 5 bij het sleutelwoord LEMON). Zo'n shift was afhankelijk van de key-setting. Hoeveel key-settings wordt de key-space genoemd. In een latere fase is de Enigma nog verbeterd wat resulteerde in een nog grotere key-space.
De Enigma had veiligheidslekken maar was voor die tijd veilig genoegd.
6. Perfect security
Bekijk onderstaande film en maak dan de opdracht.
7. Een beetje logica
In de logica, een onderdeel van de informatica, worden waarheidstabellen gebruikt. Deze tabellen worden gebruikt om te bepalen of iets waar is of niet. Een voorbeeld van een waarheidstabel is de "AND" tabel. Beide waarden moeten waar zijn om de hele bewerking waar te maken. Een waarde wordt aangeduid met een p of een q.
| P |
q |
p en q |
| 1 |
1 |
1 |
| 1 |
0 |
0 |
| 0 |
1 |
0 |
| 0 |
0 |
0 |
Je kunt zo'n tabel ook vergelijken met schakelaars die in serie zijn geschakeld. Beide schakelaars moeten ingeschakeld staan om de lamp te kunnen laten branden. Beide schakelaars inschakelen levert ook een waar op.
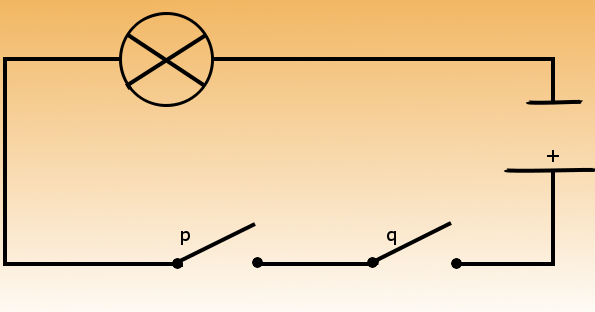
Een andere tabel is ook mogelijk op basis van "OR". Eén van beide waarden moet waar zijn om de hele bewerking waar te maken.
| p |
q |
p of q |
| 1 |
1 |
1 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
Deze tabel is vergelijkbaar met een parallelschakeling. Eén van beide schakelaars moet aanstaan om de lamp te kunnen laten branden.
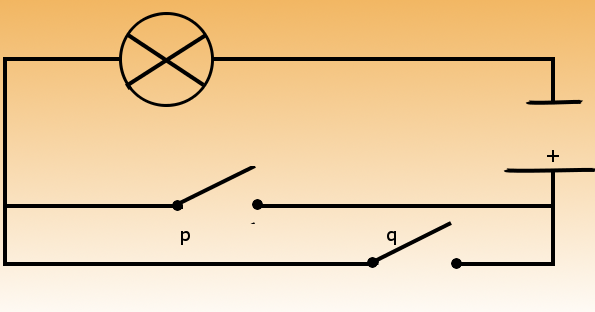
Op basis van deze tabellen is het mogelijk om encryptie toe te passen. Stel dat we de letterd d hebben. Deze is 3 waard als we ervan uitgaan dat de letter a=0. Binair levert dit het volgende 5-bits binaire getal op: 00011 (kijk eventueel in de cursus binair rekenen hoe een binair getal wordt gemaakt).
Stel nu dat we deze letter willen encrypten. Hiervoor verzinnen we ook een 5-bits key, stel 01001. De berekening met een AND-tabel gaat dan als volgt:
| p |
0 |
0 |
0 |
1 |
1 |
| q |
0 |
1 |
0 |
0 |
1 |
| p en q |
0 |
0 |
0 |
0 |
1 |
Dit levert de letter b op want b=1 en het uitgerekende binaire getal is 00001
8. De XOR tabel
Waarschijnlijk zul je moeite hebben gehad met de opdrachten uit deel 7. Je zult erachter zijn gekomen dat het vercijferen en ontcijferen moeilijkheden oplevert (welke moeilijkheden dat zijn vermeld je in je opdracht). Er is een betere tabel om voor vercijfering te gebruiken. Deze heet de Exclusieve Or of afgekort: XOR-tabel. Deze tabel is als volgt:
| p |
q |
p xor q |
| 1 |
1 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
Om zo'n schakeling te maken wordt gebruik gemaakt van een verschillende NAND-poorten. Zo'n poort werkt precies andersom als een AND-tabel. Een NAND-tabel is alleen waar, juist als p en q niet waar zijn. Door deze als hieronder te combineren kun je bovenstaande XOR-tabel of schakeling verkrijgen.
Het mooie van deze tabel is dat 50% waar is en 50% niet waar. Dat is veel beter geschikt dan de AND of OR waarheidstabellen (zie ook de opdrachten uit deel 7, als je deze goed hebt uitgevoerd snap je waarom dit zo is).
9. Encryptie met java in de praktijk
Om je ook een stukje van de praktijk te laten ervaren, laten we hieronder zien hoe je met behulp van Java-code een afbeelding kunt encrypten met behulp van een XOR-tabel. Doe als volgt:
Maak in Netbeans een nieuwe Java Application aan (dus niet een Java Web project).
Geef het de naam encrypt met kleine letters.

Maak vervolgens een nieuwe Java class en geef deze eveneens de naam Encoder, met een hoofdletter.
Geef ook alvast de package een naam. Je mag deze ook veranderen naar je eigen (domein)naam.
Kopieer nu onderstaande code in de class. Let erop dat je de package bovenaan in de class laat staan.
import java.io.FileInputStream;
import java.io.BufferedInputStream;
import java.io.FileOutputStream;
import java.io.File;
public class Encoder {
public static void main(String args[]) throws Exception {
encode("C:/temp/input.png", "C:/temp/key.txt", "c:/temp/output.png");
//encode("C:/temp/output.png","C:/temp/key.txt", "c:/temp/input.png");
}
private static void encode(String inputFile, String keyFile, String outputFile) throws Exception {
int[] key = readKey(keyFile);
BufferedInputStream in = new BufferedInputStream(new FileInputStream(inputFile), 2048);
FileOutputStream out = new FileOutputStream(outputFile);
int read = -1;
int totalRead = 0;
do {
read = in.read();
/*hieronder vindt de daadwerkelijke encryptie plaats
XOR is te bereiken met het ^ teken
***************************************************/
out.write(read ^ key[totalRead % (key.length - 1)]);
/**
* ***********************************************
*/
totalRead++;
} while (read != -1);
in.close();
out.flush();
out.close();
}
private static int[] readKey(String keyFile) throws Exception {
if ((new File(keyFile)).length() <= 0) {
throw new Exception("key size is zero!");
}
int[] fileContents = new int[(new Long((new File(keyFile)).length())).intValue() + 1];
FileInputStream in = new FileInputStream(keyFile);
int totalRead = 0;
int read = -1;
do {
read = in.read();
fileContents[totalRead] = read;
totalRead++;
} while (read != -1);
in.close();
return fileContents;
}
}
Nu zoek je een afbeelding op internet met de extensie .png en je plaatst dit ergens in een mapje, bijvoorbeeld in je downloadmapje. In onderstaand voorbeeld is de naam van de afbeelding gewijzigd in input.png. In datzelfde mapje maak je ook met kladblok (met de rechtermuisknop) een keyfile met daarin een stukje tekst. Het stukje tekst is de key. Je kunt dit ook met het kladblok doen.
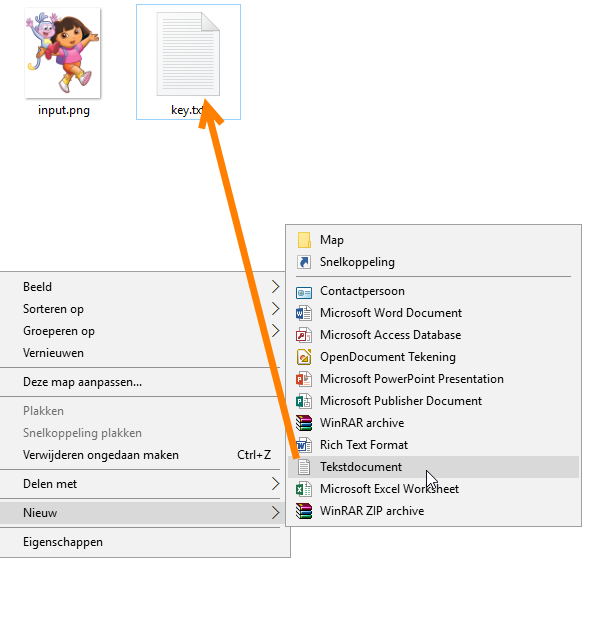
Pas nu in je script de plaats van je afbeelding en je key.txt aan. Tevens geef je in de code in Netbeans aan waar output.png moet komen te staan. Dit wordt de vercijferde afbeelding.

Draai nu het script met shift-F6 en aanschouw dat er daadwerkelijk een afbeelding output.png wordt gemaakt. Probeer deze afbeelding te lezen. Als je de input.png nu weghaalt (of even een andere naam geeft en de // voor de 2e regel weghaalt en voor de eerste regel plaatst, wordt de afbeelding weer ontcijferd.
10. antwoorden
Opdracht 2.2.1
AWESFV VAW YWYWNWFK GFVWJKUZWHL GX GH BW UGEHMLWJKQKLWWE TAFFWFVJAFYL, EGWL VAW YWYWNWFK FAWL CMFFWF TWYJABHWF.
In de zin komt de letter W 21 keer voor. Omdat de E het vaakste voorkomt in de Nederlandse taal kijken we daar als eerste naar.. Als een W een E is, is er sprake van een verschuiving van 8 plaatsen. De rotatie is dus 8.
IEMAND DIE GEGEVENS ONDERSCHEPT OF OP JE COMPUTERSYSTEEM BINNENDRINGT, MOET DIE GEGEVENS NIET KUNNEN BEGRIJPEN.
Opdracht 2.3.1
De originele tekst is:
Op een mooie Pinksterdag
Als het even kon
Liep ik met mijn dochter aan het handje in het parrekie te kuieren in de zon
Gingen madeliefjes plukken
Eendjes voeren
Eindeloos
Kijk nou toch, je jurk wordt nat
Je handjes vuil
En papa boos
Vader was een mooie held
Vader was de baas
Vader was een duidelijke mengeling van Onze Lieve Heer en Sinterklaas
Ben je bang voor ‘t hondje
Hondje bijt niet
Papa zegt dat ie niet bijt
Op een mooie Pinksterdag
Met de kleine meid
gecodeerd met madelief
Opdracht 2.7.2
Met and
b 0 0 0 0 1 a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 a 0 0 0 0 0 n 0 1 0 1 1
a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 s 1 1 1 0 1
a 0 0 0 0 0 a 0 0 0 0 0 a 0 0 0 0 0 a 0 0 0 0 0 a 0 0 0 0 0 j 0 1 0 0 1
Met or
b 0 0 0 0 1 a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 a 0 0 0 0 0 n 0 1 0 1 1
a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 s 1 1 1 0 1
b 0 0 0 0 1 l 0 1 0 1 1 l 0 1 0 1 1 l 0 1 0 1 1 a 0 0 0 0 0 1 1 1 1 1
Beide methoden zijn dus onbruikbaar.
Opdracht 2.7.3
b 0 0 0 0 1 a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 a 0 0 0 0 0 n 0 1 0 1 1
a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 n 0 1 0 1 1 a 0 0 0 0 0 s 1 1 1 0 1
b 0 0 0 0 1 k 0 1 0 1 0 l 0 1 0 1 1 l 0 1 0 1 1 a 0 0 0 0 0 o 1 0 1 1 0

