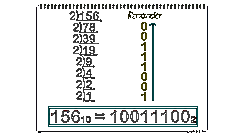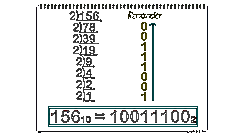1. Wat is binair rekenen
Binair rekenen gaat over het rekenen met binaire getallen. Binair staat voor 2. Dat houdt in dat een binair stelsel maar 2 getallen kent namelijk een 1 en een 0. We zeggen dan dat het grondgetal 2 is. Het grondgetal geeft het aantal tekens aan van een bepaald stelsel. Het tiental stelsel, zoals wij dat kennen, heeft 10 getallen namelijk van 0 t/m 9.
Binaire getallen worden vooral voor computers gebruikt omdat een computer vele schakelaars heeft. Een schakelaar is - normaal gesproken - ook binair namelijk aan of uit (1 of 0).
2. Een binair getal omrekenen naar een decimaal getal
Hieronder zie je een tabel met waarden.
| binair |
1 |
1 |
1 |
1 |
| decimaal |
8 |
4 |
2 |
1 |
Begin van rechts af. De eerste bit aan de rechterkant is 1 waard. Deze wordt verdubbeld en de volgende bit is 2 waard. Deze wordt verdubbeld en de volgende bit is 4 waard. Zo kun je oneindig doorgaan. In bovenstaand voorbeeld gaan we echter niet verder dan vier bits.
De decimale omzetting gebeurt door alle waarden bij elkaar op te tellen. Hieronder staat het getal 11 (8 + 2 + 1).
| binair |
1 |
0 |
1 |
1 |
| decimaal |
8 |
4 |
2 |
1 |
Je kunt een decimaal getal maar op één manier opschrijven
3. Een decimaal getal omrekenen naar een binair getal
Andersom, van een decimaal getal naar een binair getal, kan ook. Stel dat we 27, een vijf-bits binair getal, willen omrekenen. Dan maken we eerst een tabel van vijf bits en schrijven we de decimale waarden eronder.
Vervolgens gaan we kijken wat het grootste binaire getal is wat in 27 past. Dat blijkt 16 te zijn. Dit getal zetten we "aan"
Vervolgens trekken we dit van 27 af dus 27 - 16 = 11.
Wat is nu het grootste getal wat in 11 past? Dat is 8 dus die zetten we aan.
Bij elkaar komen we nu tot 16 + 8 = 24. Nu houden we 3 over. We kunnen nu 2 en 1 aanzetten en hebben het decimale getal 11011.
4. Binair optellen
Stel dat we de volgende 2 binaire getallen willen optellen:
We beginnen dan met de rechterkant: 0 + 1 = 1
Vervolgens gaan we door en tellen we 1 + 0 op.
Dit is niet moeilijk. We hebben binair uitgerekend dat 2 + 1 = 3. Maar stel nu dat we 3 + 3 binair willen uitrekenen.
We krijgen nu te maken met het volgende fenomeen. Hoeveel is 1 + 1 binair? Dat is 0. Een even aantal bits levert altijd een 0 op.
Waar blijft nu de rest want decimaal gezien is 1 + 1 = 2 en er staat 0! We moeten die 2 nog ergens kwijt. Die schrijven we bovenin de kolom die 2 waard is. We zeggen "1 onthouden".
Nu moeten we de 2e kolom gaan uitrekenen. We krijgen nu binair 1 + 1 + 1. Hoeveel is dat? Dat is 1. Een oneven aantal bits levert 1 op.
Zijn we er nu al? Nee. We hebben drie bits met decimale waarde van 2 bij elkaar opgeteld. Decimaal staat er nu 2. Waar blijft de waarde 4? Deze schrijven we in de volgende kolom met waarde 4. We zeggen "1 onthouden".
Het laatste wat we doen is de 3e kolom bij elkaar optellen. Dat is niet moeilijk want het bestaat maar uit 1 bit.
We hebben nu het juiste getal gevonden. 3 + 3 is decimaal 6 en binair staat er 6.
carrygetal
We noemen de bits die we moeten onthouden het carrygetal. In bovenstaande berekening schrijven we ook de 0 aan de rechterkant.
5. Grotere getallen binair bij elkaar optellen
Een groter binair getal bij elkaar optellen gaat op dezelfde manier. Zie onderstaand voorbeeld.
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
| 0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
| 1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
Voor de zekerheid kun je ook de decimale getallen erbij zetten.
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
| 0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
119 |
| 0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
59 |
| 1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
178 |
Het carrygetal is dus 1111 1110. Schrijf een groter binair getal altijd in vier bits gegroepeerd.
Het kan ook zijn dat je op een 9-bits getal als uitkomst uitkomt.
| |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
219 |
| |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
229 |
| 1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
448 |
6. Binaire getallen van elkaar aftrekken
Binair aftrekken heeft grote overeenkomsten met binair optellen. We beginnen weer met 4-bit. Stel dat we 0111 willen aftrekken van 1101. In de meest rechts kolom trekken we 1 van 1 af. Automatisch is de carry in de 2e kolom 0 (en in de 1e kolom ook). Deze schrijven we echter onderaan.
Nu krijgen we 0-1 en dat is 1 omdat er in de binaire wereld alleen een 0 en een 1 voorkomt. Omdat we echter als het ware "onder de 0 komen" moeten we in de 3e kolom een carry schrijven.
| 1 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
| |
1 |
0 |
0 |
| |
|
1 |
0 |
Nu krijgen we drie 1-en onder elkaar. Je krijgt dan de volgende berekening 1 - 1 = 0 en 0 - 1 is 1, dus een carry.
| 1 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
| 1 |
1 |
0 |
0 |
| |
1 |
1 |
0 |
De laatste som is makkelijk. Het is ook altijd handig om de decimale waarden erbij te schrijven en daarmee te checken of het klopt.
| 1 |
1 |
0 |
1 |
13 |
| 0 |
1 |
1 |
1 |
7 |
| 1 |
1 |
0 |
0 |
|
| 0 |
1 |
1 |
0 |
6 |
7. Hexadecimaal rekenen
Het hexadecimale getal heeft als grondgetal 16.Dat houdt dus in dat er 16 tekens zijn namelijk van 0 t/m F waarbij F 15 waard is. Het schema wordt dan als volgt:
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
Het meest rechtse teken is 0-15 waard. Het teken in de tweede kolom is 16 keer zoveel. Dus bijvoorbeeld:
9A = decimaal 9 x 16 + 10 = 144
CD=12 x 16 = 192 + 13 = 205
Hexadecimale getallen zijn erg handig bij het binair rekenen. Neem de volgende berekening:
1101 0110 + 0110 0111.
Zo te bezien is het onmogelijk om dit uit het hoofd te doen. Als we de berekening echter hexadecimaal laten zien dan wordt het al een stuk overzichtelijker.
D6 + 67
Je kunt dat als volgt berekenen. Tel eerst de meeste rechtse kolom, de 1e kolom, bij elkaar op. 6+7=13=D. Omdat je niet boven de 16 komt ontstaat er geen carry.
Nu de volgende, 2e, kolom. D + 6 = 13+6=19. Dit getal zit niet in het hexadecimale stelsel. Je moet daarom doortellen en 16 ervan af halen. Dan kom je uit op 3. De 16 schrijven we in de volgende kolom als een carry. Dit is 16 * 16 = 256 waard.
De volledige berekening is dan als volgt.
| |
D |
6 |
13*16=160+48=208 | 208+6 =214 |
| |
6 |
7 |
6*16=96 | 96+7=103 |
| 1 |
3 |
D |
256+3*16+13=317 (=214+103) |
8. Het vijftallen stelsel
Er zijn allerlei stelsel met verschillende grondgetallen. Zo is er het drie-, vier of vijftallenstelsel. Dit laatste zullen we in deze laatste leereenheid ook behandelen. Het vijftallenstelsel heeft als grondgetal 5. Er zijn dus vijf tekens namelijk van 0 t/m 4.
Hoe schrijf je nu 53? Dat gaat zo:
Ook bij dit stelsel wordt de kolom telkens met het grondgetal vermenigvuldigt. Het decimale getal 53 kun je terugrekenen door telkens de waarde van de grootste kolom te nemen. Dus in 53 past 2 * 25. Dan hou je 3 over. Daar past niet 5 in dus wordt dit vakje 0. Als laatste krijg je 3 van 1.