1. Overzicht van deze cursus

Een datastructuur is een structuur om gegevens, de data, in te kunnen opbergen. Een ander woord voor datastructuur is collectie. Dit verwijst naar het Collection framework van Java zoals hieronder is getoond.

In deze cursus ga je alles leren over datastructuren en zullen we verschillende voorbeelden uitwerken hoe we deze kunnen gebruiken.

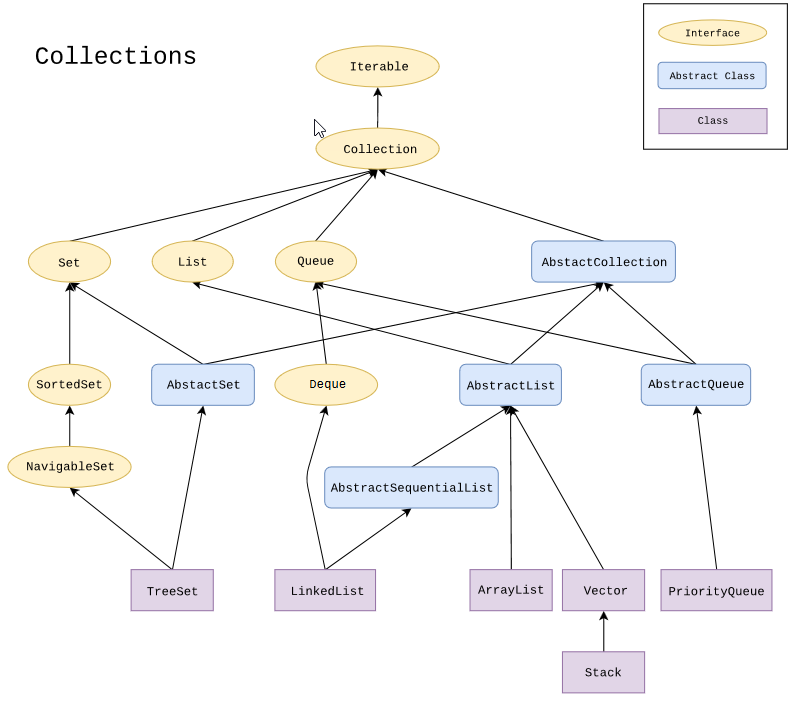
bron afbeelding: Wikipedia

Je ziet in deze afbeelding twee verschillende soorten structuren:

• Abstract classes en Interfaces. Dit zijn classes die methoden bevatten die nog niet zijn gedefinieerd maar die wel verplicht moeten worden overgenomen worden in een subclass.
• Subclasses. Hierin gebeurt het echte werk.

We zullen in de cursus diverse classes behandelen zoals een ArrayList, een LinkedList of een Queue.

abstract classes en interfaces

De overeenkomst tussen een abstract class en een interface is dat van beide soorten classes geen objecten gemaakt kunnen worden. Voor het maken van een object is er altijd een onderliggende, overervende, class. Een interface is een speciale abstract class. Deze bevat alleen methoden die moeten worden gedefinieerd in onderliggende class. Men noemt een interface daarom ook wel een contract. Je bent verplicht om de gedefinieerde methoden over te nemen.

Hieronder een voorbeeld van een abstract class.

public abstract class Bike {

    public Bike() {
        System.out.println("Bike is created");
    }

    public abstract void run();
}

Als de class Citybike wordt gedefinieerd dan is deze verplicht om de methode run() over te nemen. De class zelf kan nog wel iets doen (in dit geval gebeurt dat in de constructor die de melding "Bike is created"  geeft.

public class Citybike extends Bike {

    public void run() {
        System.out.println("This is a citybike");
    }

    public static void main(String args[]) {
        Bike bike = new Citybike();
        bike.run();
    }
} 

public class Mountainbike extends Bike {

    public void run() {
        System.out.println("This is a mountainbike");
    }

    public static void main(String args[]) {
        Bike bike = new Mountainbike();
        bike.run();
    }
}

2. Wat is een algoritme

De naam algoritme is een verbastering van de naam Al-Khwarizmi. Deze Arabische wiskundige schreef in de negende eeuw een boek over getallen Het boekje is in de twaalfde eeuw in Spanje in het Latijn vertaald en de naam Al-Khwarizmi werd daarbij verbasterd tot het woord ‘algorismi’. Hieruit is later het woord algoritme ontstaan.

Algoritme betekent in basis rekenmethode of rekenrecept. Als een computer iets uit moet rekenen, dan heeft hij daarvoor een algoritme nodig. In de loop der tijd werd het woord algoritme een algemene term voor methoden die stap voor stap beschrijven hoe een probleem moet worden opgelost.

Algoritmes werden al ver voor de uitvinding van de computer gemaakt. Stel dat we bijvoorbeeld van twee getallen de grootste gemene deler (GGD) willen vinden. Het algoritme hiervoor is als volgt:

1. Neem twee getallen, bijvoorbeeld 75 en 105.
2. Ontbind deze in priemfactoren dus
   • 75=3x5x5 (ieder getal is maar op één manier in priemfactoren te ontbinden)
   • 105=3x5x7
3. Neem nu de gezamelijke priemfactoren. Deze zijn 3x5.
4. Vermenigvuldig deze met elkaar en we komen op 15. Dit is de GGD.

We kunnen ook een ander algoritme nemen, het algoritme van Euclides:

1. Deel het grootste getal door het kleinste getal dus 105 delen door 75 = 1 rest 30
2. Doe dit opnieuw door het kleinste getal te delen door de rest dus 75 delen door 30 = 2 rest 15
3. Opnieuw 30 delen door 15 = 2 rest 0. Zodra de rest 0 is, is de GGD gevonden.

Een ander kenmerk van een algortime is dat het zichzelf kan herhalen. Dit is heel goed te zien bij het algoritme van Euclides, zeker als we daar grotere getallen nemen. We kunnen dat algoritme nog wat formeler opschrijven.

• Zolang de rest ongelijk is aan 0
  • deel het grootste getal door het kleinste getal
• Zodra de rest is 0
  • het deelgetal is de GGD.

3. Een nieuw java project

In deze cursus zullen we veel oefenen in de praktijk. We doen dit in met behulp van Netbeans. Hoe Netbeans werkt staat uitgebreider beschreven in de cursus Netbeans.

Maak een nieuw Java project in Netbeans. Noem het nieuwe project Datastructures zoals de naam van deze cursus.

Hierna heb je een project met één Java Class die automatisch wordt geopend. Verwijder al het commentaar. Als je al het commentaar hebt verwijderd hou je de volgende class over:

package arrays;

public class Datastructures {

    public static void main(String[] args) {

    }
}

Merk op dat we de package arrays hebben genoemd. Standaard maakt Netbeans de package datastructures aan. Met de rechtermuisknop (refactor) kun je de naam van de package veranderen.

4. Arrays maken en uitprinten

Een array (rij) is een datastructuur die bestaat uit een lijst van elementen van hetzelfde type. Ieder element in een array kan worden opgezocht door middel van de index. De array behoort niet tot het Collections Framework maar zit standaard in de basiselementen van Java. Veel classes van het Collections Framework zijn gebaseerd op arrays. Het is daarom van belang om hiermee te oefenen.

Om zo'n array te maken en te testen maken we in de class Datastructures de volgende variabele:

public static int[] primes = {2, 3, 5, 7, 11, 13, 17, 19};

Dit noemen we een array van het type int. We hebbe deze static en public gemaakt zodat de variabele, zonder dat we eerst een object moeten aanmaken,  De array vullen we meteen met een alle priemgetallen onder de 20.

 We hebben nu een array die als volgt in het geheugen staat:

primes

data	2	3	5	7	11	13	17	19
index	0	1	2	3	4	5	6	7

 De index geeft de plaats van het element aan. Dus stel dat we het priemgetal 13 zouden willen uitprinten dan kan dat met de volgende toegevoegde code die we plaatsen in de main method:

System.out.println(primes[5]);

Het resultaat is dan 13. 

aanwijzing: je kunt de class runnen met shift-F6. Het resultaat is te zien in de output tab.

Om de hele array te lezen kunnen we gebruik maken van een forloop waarbij we de teller i (van integer) gebruiken om de positie uit te lezen.

for (int i = 0; i < primes.length; i++) {
    System.out.print(primes[i]);
}

5. complexiteit van een algoritme

De complexiteit van een algoritme wordt uitgedrukt in tijdseenheden. Een tijdseenheid is op een snellere computer minder groot dan op een langzame computer. Het heeft daarom geen zin om de snelheid van een algoritme te meten in tijd. Deze is in principe niet van belang. Wat wel van belang is, is hoeveel bewerkingen een algoritme moet toepassen om een bepaald doel te bereiken.

Stel dat we een array hebben gemaakt zoals in voorgaande les:

public static int[] primes = {2, 3, 5, 7, 11, 13, 17, 19};

Hoeveel tijd kost het nu om het 5e getal uit te printen. Dat is precies één bewerking namelijk:

System.out.println(primes[4]);

We geven dit aan met het big O symbool: 0(1) waarbij de 1 staat voor precies één tijdseenheid.

O(n)

Stel nu dat we willen onderzoeken of het getal 13 in de array staat. Dit doen we met de volgende pseude code:

index=0; 
number=13 //het te zoeken getal
while index < primes.length
    if(primes[index]==number)
    return number
end while
return 0;

Omdat we niet weten of het getal voor- of achteraan in de array staat gaan we uit van het worst case scenario, namelijk dat het getal achteraan in de array staat of helemaal niet is te vinden in de array. We geven dit aan met O(n) waarbij n staat voor de lengte van de data, in ons geval de array. We kunnen ook zeggen dat dit de bovengrens is, dus de maximale tijd die nodig is om het getal te vinden.

Naast het worst case scenario is er ook het best case scenario. Dit geven we aan met het $\mathrm{\Omega }$(n). We spreken dit uit als Omega(n). We kunnen ook zeggen dat dit de ondergrens is, dus de minimale tijd die nodig is om het getal te vinden.

Als we zeker weten dat de gehele array doorlopen moet worden dat spreken we van $\mathrm{\Theta }$(n). We spreken dit uit als Theta(n).

Eigenlijk moeten we het nog anders opschrijven namelijk: O(f(n)) waarbij we de volgende waarden kunnen uitlezen:

• n is de lengte van de data, dus in dit geval de lengte van de array.
• f staat voor functie met n als parameter. Het gaat hierbij om het algoritme met n (of de array) als parameter.
• O is de bovengrens, dus het worst case scenario.

Over het algemeen wordt de f niet geschreven. De complexiteit van een algoritme wordt alleen aangegeven met n.

Bovenstaande complexiteit is een lineaire groei: de groei is afhankelijk van de grootte van n. In een grafiek ziet dat er zo uit:

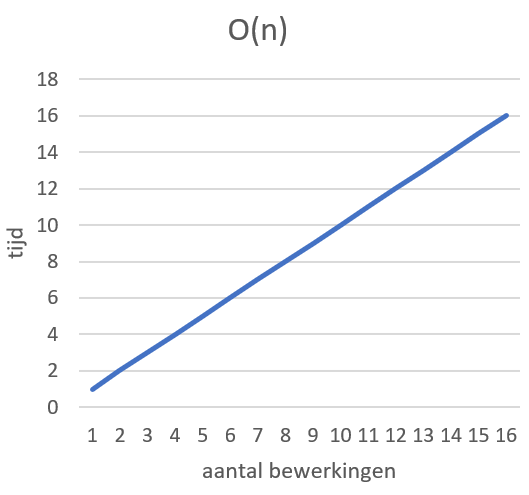
O(n²)

Stel dat we de volgende array maken:

public static String[] spreads = {"Cheese", "Bread", "Olives", "Hazelnut", "Chocolate"};

We willen nu deze 5 ingrediënten met elkaar combineren op een dusdanige manier dat er geen dubbele combinaties voorkomen. Dus de output moet als volgt zijn:

Cheese with Bread
Cheese with Olives
Cheese with Hazelnut
Cheese with Chocelate
Bread with Olives
Bread with Hazelnut
Bread with Chocelate
Olives with Hazelnut
Olives with Chocelate
Hazelnut with Chocelate

Met welk algoritme gaan we dit bereiken? We geven hier de grotendeels de code:

public static void main(String[] args) {
    for (int i = 0; i < spreads.length; i++) {
        for (int j = ??; j < ??; j++) {
            if (spreads[i]!= spreads[j]) {
                System.out.println(spreads[i] + " with " + spreads[j]);
            }
        }
    }
}

In de onderstaande opdracht maak je de code werkend. Merk op dat we nu te maken hebben met een dubbele for-loop. Voor elke spreads[i] wordt spreads[j] vergeleken. Het maakt daarbij niet uit wat de grootte is van j. We zeggen dat de complexiteit in de orde van grootte van O(n²) is. We geven ook de bijbehorende grafiek:

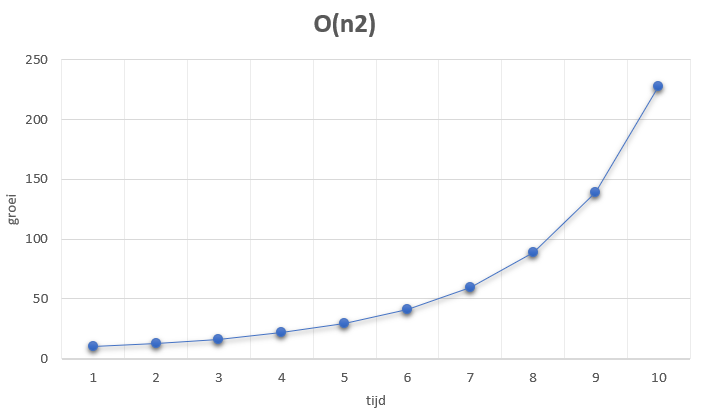
6. Priemgetallen vinden

We zullen nu met behulp van een forloop en een array een algoritme maken wat priemgetallen kan vinden. Hiervoor maken we een array met 20 getallen met behulp van een for-loop. Dat kan met de onderstaande code. Let op de vraag bij het commentaar. De code is niet compleet. Deze vraag komt ook terug in de opdracht van deze les. Je kunt proberen de code vast werkend te maken.

int maxNumbers = 20;
boolean primes[] = new boolean[maxNumbers + 1];

/**
 * Maak alle nummers priem. Wat moet er staan op de plaats van het
 * vraagteken?
 */
for (int i = 1; i <= maxNumbers; i++) {
    primes[ ?] = true;
}

Hoe vinden we de priemgetallen. We kunnen hiervoor de zeef van Eratosthenes nemen. Dit werkt als volgt:

1. Begin van de reeks getallen (in ons geval tot en met 20) met het getal 2 en schrap alle veelvouden, 4,6,8 .....20. We hebben ons eerste priemgetal gevonden, namelijk 2.
2. Verhoog het getal met 1, dus dat wordt 3, en schrap opnieuw alle veelvouden die nog niet zijn geschrapt: 9, 15. Het volgende priemgetal is 3.
3. Herhaal stap 2. 4 is geschrapt dus we moeten naar getal 5. Alle veelvouden daarvan zijn al geschrapt.

De code voor dit algoritme is hieronder te bekijken. Let op de vraagtekens en het commentaar met uitleg van de code.

/**
 * @1. starten met 2,
 * @2. maak er een veelvoud van (currentNumber*currentNumber)
 * @3.check of dit niet voorbij het ingestelde maxNumber gaat
 * @4. verhoog het currentNumber met 1 Wat moet er staan op de plaats
 * van het vraagteken?
 */
for (int currentNumber = 2; (currentNumber * currentNumber) <= maxNumbers; currentNumber++) {
    //check of de postie true is. Wat moet er staan op de plaats van het vraagteken?
    if (primes[ ?]) {
        /**
         * @1. Maak een variabele deleteNumber waarbij de startwaarde
         * het veelvoud is van het te checken getal (int deleteNumber =
         * currentNumber * currentNumber)
         * @2. Ga door met het maken veelvouden door bij deleteNumber
         * telkens het currentNumber op te tellen.
         */
        for (int deleteNumber = currentNumber * currentNumber; deleteNumber <= maxNumbers; deleteNumber += currentNumber) {
            System.out.println(deleteNumber);
            primes[ ?] = false;
        }
    }
}

Als laatste printen we al true-posities van de array.

System.out.print("de priemgetallen zijn: ");
/**
 * @ Print de priemgetallen. Wat moet er staan op de plaats van het
 * vraagteken?
 */
for (int i = 2; i < ?; i++) {
    if (primes[ ?]) {
        System.out.print("  " + i);

    }
}

7. De array praktisch toepassen op een scorelijst

Een andere praktische toepassing van een array is het bijhouden van een scorelijst. Tot nu toe hebben we alleen primitieve variabelen aan de array toegevoegd. In deze les zullen we objecten in de array opslaan. We maken in de package datastructures hiervoor eerst de volgende class Score. Score is een eenvoudige class met twee variabelen.

public class Score {

    private String name;
    private int score;

    /**
     * @param name name
     * @param score score
     */
    public Score(String name, int score) {
        this.name = name;
        this.score = score;
    }

    public String getName() {
        return  this.name;
    }

    public int getScore() {
        return this.score;
    }

    public String toString() {
        return "(" + this.name + ", " + this.score + ")";
    }
}

Je ziet dat we in de class een methode toString() hebben gemaakt. Dit is om het object te kunnen printen.

We maken ook een class ScoreList waarin we de individuele scores gaan bijhouden. In deze class kunnen meerdere classes Score worden aangemaakt.

public class ScoreList {

    public final int maxScores = 10;
    private int countScores;
    private Score[] scoreList;

    public ScoreList() {
        //hier code om een nieuwe array te maken met maximaal 10 objecten
        //...
    }

    public String toString() {
        String string = "[";
        for (int i = 0; i < countScores; i++) {
            if (i > 0) {
                string += ", ";
            }
            string += scoreList[i];
        }
        return string + "]";
    }
}

Nog een paar opmerkingen over deze twee classes:

• de class Score is bedoeld om één score te maken op iemands gebruikersnaam
• In de class Scorelist kunnen maximaal 10 scores worden opgeslagen. Je kunt de variabele maxScores zien als een instelling. 
• De variabele countScores is een hulpvariabele om het aantal opgeslagen scores bij te houden. 

8. Een score toevoegen

Met de onderstaande code wordt het mogelijk om een score toe te voegen:

public void addScore(Score score) {
        //we vragen de waarde van de nieuwe score op en plaatsen dit in de newScore variable
        int newScore = score.getScore();
        //als de lijst niet groter is dan 10
        if (countScores < this.scoreList.length
                //en de score groter is dan de laatste in de lijst
                || newScore > scoreList[countScores - 1].getScore()) {
            //verhoog het score aantal
            if (countScores < this.scoreList.length) {
                countScores++;
            }
        }
        //stel de teller in aan de hand van de tot dan toe ingevoerde scores
        int i = countScores - 1;

        //hier wordt gekeken op welke plaats de nieuwe score groter is
        //vervolgens wordt de oude score één voor één een plaats lager gezet
        while (i > 0 && scoreList[i - 1].getScore() < newScore) {
            scoreList[i] = scoreList[i - 1];
            i--;
        }
        //hier wordt de nieuwe score toegevoegd aan de vrijgekomen plaats
        scoreList[i] = score;
    }

Vervolgens kunnen we de code uitproberen in de main van Datastructures.java

    public static void main(String[] args) {

        ScoreList scoreList = new ScoreList();
        scoreList.addScore(new Score("Piet", 45));
        scoreList.addScore(new Score("John", 43));
        scoreList.addScore(new Score("Klaas", 79));
        scoreList.addScore(new Score("Kees", 2));
        scoreList.addScore(new Score("Jan", 21));
        scoreList.addScore(new Score("Jan", 21));
        scoreList.addScore(new Score("Janneke", 121));
        scoreList.addScore(new Score("Jan", 12));
        scoreList.addScore(new Score("Jan", 221));
        scoreList.addScore(new Score("Nelleke", 21));
        scoreList.addScore(new Score("Birgit", 321));
        System.out.println(scoreList);
    }

Wat duidelijk wordt in bovenstaande algoritmes is dat bij het invoegen van een nieuwe score, de overige scores moeten worden opgeschoven. Dit speelt een belangrijke rol in de snelheid van het algoritme. 

9. Een score verwijderen

We kunnen ook een script maken die een score verwijdert. Voeg deze code toe en kijk vervolgens eerst naar de bijbehorende lesopdracht.

public Score remove(int i) throws IndexOutOfBoundsException {
        //eerst kijken we of de arraypositie niet kleiner dan 0 is
        //of groter is dan de index van de array
        //zo ja dan gooien we een exception op
        if (i < 0 || i >= countScores) {
            throw new IndexOutOfBoundsException("Invalid index: " + i);
        }
        //de oude score bewaren we zodat we zeker weten welke score er wordt verwijderd
        Score tempScore = scoreList[i];
        //hier tellen we op. Vanaf de lege plaats worden alle scores een plaats teruggeschovend
        for (int j = i; j < countScores; j++) {
            scoreList[j] = scoreList[j+1];
        }
        //de laatste plaats wordt leeggegemaakt
        scoreList[countScores - 1] = null;
        countScores--;
        return tempScore;
    }

 De code kunnen we vervolgens in de main werkend zien.

        System.out.println(scoreList.remove(2));
        System.out.println(scoreList.toString());

Met het volgende resultaat:

[(Birgit, 321), (Jan, 221), (Janneke, 121), (Klaas, 79), (Piet, 45), (John, 43), (Jan, 21), (Jan, 21), (Nelleke, 21), (Jan, 12)]
(Janneke, 121)
[(Birgit, 321), (Klaas, 79), (Piet, 45), (John, 43), (Jan, 21), (Jan, 21), (Nelleke, 21), (Jan, 12), (Nelleke, 21)]

conclusie

Je ziet dat we met behulp van relatief eenvoudige technieken al een vrij krachtige datastructuur kunnen bouwen. Toch zitten er wel wat nadelen aan deze manier van werken:

• we moeten vooraf aangeven hoe groot de array gaat worden.

10. Antwoorden 1- 5

Dit onderdeel is uitgeschakeld door de docent.

11. Antwoorden 6 - 9

Dit onderdeel is uitgeschakeld door de docent.